Задачи с плоскостью. Проекции точки и прямой, принадлежащих плоскости общего положения Если точка принадлежит двум плоскостям то
Признаки принадлежности хорошо известны из курса планиметрии. Наша задача рассмотреть их применительно к проекциям геометрических объектов.
Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости.
Принадлежность прямой плоскости определяется по одному из двух признаков:
а) прямая проходит через две точки, лежащие в этой плоскости;
б) прямая проходит через точку и параллельна прямой, лежащим в этой плоскости.
Используя эти свойства, решим в качестве примера задачу. Пусть плоскость задана треугольником АВС . Требуется построить недостающую проекцию D 1 точки D , принадлежащей этой плоскости. Последовательность построений следующая (рис. 2.5).
Рис. 2.5. К построению проекций точки, принадлежащей плоскости
Через точку D 2 проводим проекцию прямой d , лежащей в плоскости АВС , пересекающую одну из сторон треугольника и точку А 2 . Тогда точка 1 2 принадлежит прямым А 2 D 2 и C 2 В 2 . Следовательно, можно получить ее горизонтальную проекцию 1 1 на C 1 В 1 по линии связи. Соединив точки 1 1 и А 1 , получаем горизонтальную проекцию d 1 . Ясно, что точка D 1 принадлежит ей и лежит на линии проекционной связи с точкой D 2 .
Достаточно просто решаются задачи на определение принадлежности точки или прямой плоскости. На рис. 2.6 показан ход решения таких задач. Для наглядности изложения задачи плоскость задаем треугольником.

Рис. 2.6. Задачи на определение принадлежности точки и прямой плоскости.
Для того, чтобы определить принадлежит ли точка Е плоскости АВС , проведем через ее фронтальную проекцию Е 2 прямую а 2 . Считая, что прямая а принадлежит плоскости АВС , построим ее горизонтальную проекцию а 1 по точкам пересечения 1 и 2. Как видим (рис. 2.6, а), прямая а 1 не проходит через точку Е 1 . Следовательно, точка Е АВС .
В задаче на принадлежность прямой в плоскости треугольника АВС (рис. 2.6, б), достаточно по одной из проекций прямой в 2 построить другую в 1 * считая, что в АВС . Как видим, в 1 * и в 1 не совпадают. Следовательно, прямая в АВС .
2.4. Линии уровня в плоскости
Определение линий уровня было дано ранее. Линии уровня, принадлежащие данной плоскости, называются главными . Эти линии (прямые) играют существенную роль при решении ряда задач начертательной геометрии.
Рассмотрим построение линий уровня в плоскости, заданной треугольником (рис. 2.7).

Рис. 2.7. Построение главных линий плоскости, заданной треугольником
Горизонталь плоскости АВС начинаем с вычерчивания ее фронтальной проекции h 2 , которая, как известно, параллельна оси ОХ . Поскольку эта горизонталь принадлежит данной плоскости, то она проходит через две точки плоскости АВС , а именно, точки А и 1. Имея их фронтальные проекции А 2 и 1 2 , по линии связи получим горизонтальные проекции (А 1 уже есть) 1 1 . Соединив точки А 1 и 1 1 , имеем горизонтальную проекцию h 1 горизонтали плоскости АВС . Профильная проекция h 3 горизонтали плоскости АВС будет параллельна оси ОХ по определению.
Фронталь плоскости АВС строится аналогично (рис. 2.7) с той лишь разницей, что ее вычерчивание начинается с горизонтальной проекции f 1 , так как известно, что она параллельна оси ОХ. Профильная проекция f 3 фронтали должна быть параллельна оси ОZ и пройти через проекции С 3 , 2 3 тех же точек С и 2.
Профильная линия плоскости АВС имеет горизонтальную р 1 и фронтальную р 2 проекции, параллельные осям OY и OZ , а профильную проекцию р 3 можно получить по фронтальной, используя точки пересечения В и 3 с АВС .
При построении главных линий плоскости необходимо помнить лишь одно правило: для решения задачи всегда нужно получить две точки пересечения с данной плоскостью. Построение главных линий, лежащих в плоскости, заданной иным способом, ничуть не сложнее рассмотренного выше. На рис. 2.8 показано построение горизонтали и фронтали плоскости, заданной двумя пересекающимися прямыми а ив .

Рис. 2.8. Построение главных линий плоскости, заданной пересекающимися прямыми.
Положение плоскости в пространстве определяется:
- тремя точками, не лежащими на одной прямой;
- прямой и точкой, взятой вне прямой;
- двумя пересекающимися прямыми;
- двумя параллельными прямыми;
- плоской фигурой.
В соответствии с этим на эпюре плоскость может быть задана:
- проекциями трёх точек, не лежащих на одной прямой (Рисунок 3.1,а);
- проекциями точки и прямой (Рисунок 3.1,б);
- проекциями двух пересекающихся прямых (Рисунок 3.1,в);
- проекциями двух параллельных прямых (Рисунок 3.1,г);
- плоской фигурой (Рисунок 3.1,д);
- следами плоскости;
- линией наибольшего ската плоскости.
Рисунок 3.1 – Способы задания плоскостей
Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.
Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.
Плоскость общего положения может иметь три следа: горизонтальный – απ 1 , фронтальный – απ 2 и профильный – απ 3 , которые она образует при пересечении с известными плоскостями проекций: горизонтальной π 1 , фронтальной π 2 и профильной π 3 (Рисунок 3.2).

Рисунок 3.2 – Следы плоскости общего положения
3.2. Плоскости частного положения
Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.
Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.
Свойство проецирующей плоскости : все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).

Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А , В , С ; линии АС , АВ , ВС ; плоскость треугольника АВС
Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).
Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).
Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций .
Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями .
Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).
Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).
Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).

Рисунок 3.4 – Эпюры плоскостей частного положения
3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости
Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5).
Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).

Рисунок 3.5 – Принадлежность точки плоскости
α = m // n
D ∈ n ⇒ D ∈ α

Рисунок 3.6 – Принадлежность прямой плоскости
Упражнение
Дана плоскость, заданная четырехугольником (Рисунок 3.7, а). Необходимо достроить горизонтальную проекцию вершины С .
 |
|
| а | б |
Рисунок 3.7 – Решение задачи
Решение :
- ABCD – плоский четырехугольник, задающий плоскость.
- Проведём в нём диагонали AC и BD (Рисунок 3.7, б), которые являются пересекающимися прямыми, также задающими ту же плоскость.
- Согласно признаку пересекающихся прямых, построим горизонтальную проекцию точки пересечения этих прямых — K по её известной фронтальной проекции: A 2 C 2 ∩ B 2 D 2 =K 2 .
- Восстановим линию проекционной связи до пересечения с горизонтальной проекцией прямой BD : на проекции диагонали B 1 D 1 строим К 1 .
- Через А 1 К 1 проводим проекцию диагонали А 1 С 1 .
- Точку С 1 получаем, посредством линии проекционной связи до пересечения её с горизонтальной проекцией продолженной диагонали А 1 К 1 .
3.4. Главные линии плоскости
В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).
Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.
Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π 1) (Рисунок 3.8, а; 3.9).
Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π 2) (Рисунок 3.8, б; 3.10).
Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π 3) (Рисунок 3.8, в; 3.11).

Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником

Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами

Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами

Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами
3.5. Взаимное положение прямой и плоскости
Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.
3.5.1. Параллельность прямой плоскости
Признак параллельности прямой плоскости : прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).

Рисунок 3.12 – Параллельность прямой плоскости
3.5.2. Пересечение прямой с плоскостью
Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:
- Заключить прямую а во вспомогательную плоскость β (в качестве вспомогательной плоскости следует выбирать плоскости частного положения);
- Найти линию пересечения вспомогательной плоскости β с заданной плоскостью α;
- Найти точку пересечения заданной прямой а с линией пересечения плоскостей MN .

Рисунок 3.13 – Построение точки встречи прямой с плоскостью
Упражнение
Заданы: прямая АВ общего положения, плоскость σ⊥π 1 . (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.
Решение :
- Плоскость σ – горизонтально-проецирующая, следовательно, горизонтальной проекцией плоскости σ является прямая σ 1 (горизонтальный след плоскости);
- Точка К должна принадлежать прямой АВ ⇒ К 1 ∈А 1 В 1 и заданной плоскости σ ⇒ К 1 ∈σ 1 , следовательно, К 1 находится в точке пересечения проекций А 1 В 1 и σ 1 ;
- Фронтальную проекцию точки К находим посредством линии проекционной связи: К 2 ∈А 2 В 2 .

Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения
Упражнение
Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).
Требуется построить точку пересечения прямой EF с плоскостью σ.
 |
|
| а | б |
Рисунок 3.15 – Пересечение прямой с плоскостью
- Заключим прямую EF во вспомогательную плоскость, в качестве которой воспользуемся горизонтально-проецирующей плоскостью α (Рисунок 3.15, а);
- Если α⊥π 1 , то на плоскость проекций π 1 плоскость α проецируется в прямую (горизонтальный след плоскости απ 1 или α 1), совпадающую с E 1 F 1 ;
- Найдём прямую пересечения (1-2) проецирующей плоскости α с плоскостью σ (решение подобной задачи будет рассмотрено );
- Прямая (1-2) и заданная прямая EF лежат в одной плоскости α и пересекаются в точке K .
Алгоритм решения задачи (Рисунок 3.15, б):
Через EF проведем вспомогательную плоскость α:
3.6. Определение видимости методом конкурирующих точек
При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π 1 или π 2 .
Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций .
Необходимо отдельно определить видимость на каждой плоскости проекций.
Видимость на π 2 (рис. 3.15)
Выберем точки, конкурирующие на π 2 – точки 3 и 4. Пусть точка 3∈ВС∈σ , точка 4∈EF .
Чтобы определить видимость точек на плоскости проекций π 2 надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π 2 .
Направление взгляда на π 2 показано стрелкой.
По горизонтальным проекциям точек 3 и 4, при взгляде на π 2 , видно, что точка 4 1 располагается ближе к наблюдателю, чем 3 1 .
4 1 ∈E 1 F 1 ⇒ 4∈EF ⇒ на π 2 будет видима точка 4, лежащая на прямой EF , следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K
Видимость на π 1
Для определения видимости выберем точки, конкурирующие на π 1 – точки 2 и 5.
Чтобы определить видимость точек на плоскости проекций π 1 надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π 1 .
Направление взгляда на π 1 показано стрелкой.
По фронтальным проекциям точек 2 и 5, при взгляде на π 1 , видно, что точка 2 2 располагается ближе к наблюдателю, чем 5 2 .
2 1 ∈А 2 В 2 ⇒ 2∈АВ ⇒ на π 1 будет видима точка 2, лежащая на прямой АВ , следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.
Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.
3.7. Перпендикулярность прямой плоскости
Признак перпендикулярности прямой плоскости : прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.
 |
|
| а | б |
Рисунок 3.16 – Задание прямой, перпендикулярной плоскости
Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)
Теорема доказывается через теорему о проецировании прямого угла в частном случае.
Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).
Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K .
- Построим горизонталь и фронталь в плоскости σ=ΔАВС : A-1 ∈σ; A-1 //π 1 ; С-2 ∈σ; С-2 //π 2 .
- Восстановим из точки K перпендикуляр к заданной плоскости: p 1 ⊥h 1 и p 2 ⊥f 2 , или p 1 ⊥απ 1 и p 2 ⊥απ 2
3.8. Взаимное положение двух плоскостей
3.8.1. Параллельность плоскостей
Две плоскости могут быть параллельными и пересекающимися между собой.
Признак параллельности двух плоскостей : две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
Упражнение
Задана плоскость общего положения α=ΔАВС и точка F ∉α (Рисунок 3.17).
Через точку F провести плоскость β, параллельную плоскости α.

Рисунок 3.17 – Построение плоскости, параллельной заданной
Решение :
В качестве пересекающихся прямых плоскости α возьмем, например, стороны треугольника АВ и ВС.
- Через точку F проводим прямую m , параллельную, например, АВ .
- Через точку F , или же через любую точку, принадлежащую m , проводим прямую n , параллельную, например, ВС , причём m∩ n=F .
- β = m ∩n и β//α по определению.
3.8.2. Пересечение плоскостей
Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.
Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.
Упражнение
Две плоскости α и β заданы следами (Рисунок 3.18). Построить линию пересечения плоскостей.

Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами
Порядок построения линии пересечения плоскостей :
- Найти точку пересечения горизонтальных следов — это точка М (её проекции М 1 и М 2 , при этом М 1 =М , т.к. М – точка частного положения, принадлежащая плоскости π 1).
- Найти точку пересечения фронтальных следов — это точка N (её проекции N 1 и N 2 , при этом N 2 = N , т.к. N – точка частного положения, принадлежащая плоскости π 2).
- Построить линию пересечения плоскостей, соединив одноименные проекции полученных точек: М 1 N 1 и М 2 N 2 .
М N – линия пересечения плоскостей.
Упражнение
Задана плоскость σ = ΔАВС , плоскость α – горизонтально- проецирующая (α⊥π 1) ⇒α 1 – горизонтальный след плоскости (Рисунок 3.19).
Построить линию пересечения этих плоскостей.
Решение :
Так как плоскость α пересекает стороны АВ и АС треугольника АВС , то точки пересечения K и L этих сторон с плоскостью α являются общими для обеих заданных плоскостей, что позволит, соединив их, найти искомую линию пересечения.
Точки могут быть найдены как точки пересечения прямых с проецирующей плоскостью: находим горизонтальные проекции точек K и L , то есть K 1 и L 1 , на пересечении горизонтального следа (α 1) заданной плоскости α с горизонтальными проекциями сторон ΔАВС : А 1 В 1 и A 1 C 1 . После чего посредством линий проекционной связи находим фронтальные проекции этих точек K 2 и L 2 на фронтальных проекциях прямых АВ и АС . Соединим одноимённые проекции: K 1 и L 1 ; K 2 и L 2 . Линия пересечения заданных плоскостей построена.
Алгоритм решения задачи :
KL – линия пересечения ΔАВС и σ (α∩σ = KL ).

Рисунок 3.19 – Пересечение плоскостей общего и частного положения
Упражнение
Заданы плоскости α = m//n и плоскость β = ΔАВС (Рисунок 3.20).
Построить линию пересечения заданных плоскостей.
Решение :
- Чтобы найти точки, общие для обеих заданных плоскостей и задающие линию пересечения плоскостей α и β, необходимо воспользоваться вспомогательными плоскостями частного положения.
- В качестве таких плоскостей выберем две вспомогательные плоскости частного положения, например: σ // τ; σ⊥π 2 ; τ⊥π 2 .
- Вновь введённые плоскости пересекаются с каждой из заданных плоскостей α и β по прямым, параллельным друг другу, так как σ // τ:
— результатом пересечения плоскостей α, σ и τ являются прямые (4-5) и (6-7);
— результатом пересечения плоскостей β, σ и τ являются прямые (3-2) и (1-8).
- Прямые (4-5) и (3-2) лежат в плоскости σ; точка их пересечения М одновременно лежит в плоскостях α и β, то есть на прямой пересечения этих плоскостей;
- Аналогично находим точку N , общую для плоскостей α и β.
- Соединив точки M и N , построим прямую пересечения плоскостей α и β.

Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)
Алгоритм решения задачи :
Упражнение
Заданы плоскости α = ΔАВС и β = a //b . Построить линию пересечения заданных плоскостей (Рисунок 3.21).
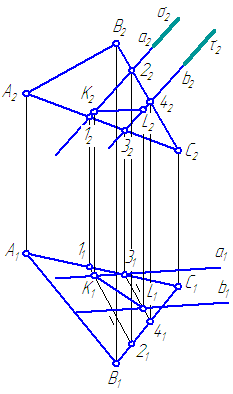
Рисунок 3.21 Решение задачи на пересечение плоскостей
Решение :
Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π 2 , заключив прямую a во вспомогательную плоскость σ (σ∈a ). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а . Следовательно (1-2)∩а =K .
Точка К принадлежит обеим плоскостям α и β.
Следовательно, точка K , является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β.
Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π 2 (τ∈b ).
Соединив точки K и L , получим прямую пересечения плоскостей α и β.
3.8.3. Взаимно перпендикулярные плоскости
Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.
Упражнение
Задана плоскость σ⊥π 2 и прямая общего положения – DE (Рисунок 3.22)
Требуется построить через DE плоскость τ⊥σ.
Решение .
Проведём перпендикуляр CD к плоскости σ – C 2 D 2 ⊥σ 2 (на основании ).
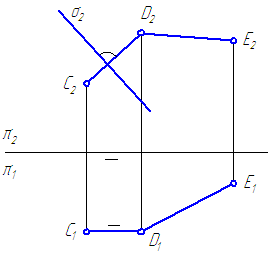
Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости
По теореме о проецировании прямого угла C 1 D 1 должна быть параллельна оси проекций. Пересекающиеся прямые CD∩ DE задают плоскость τ. Итак, τ⊥σ.
Аналогичные рассуждения, в случае плоскости общего положения.
Упражнение
Задана плоскость α = ΔАВС и точка K вне плоскости α.
Требуется построить плоскость β⊥α, проходящую через точку K .
Алгоритм решения (Рисунок 3.23):
- Построим горизонталь h и фронталь f в заданной плоскости α = ΔАВС ;
- Через точку K проведём перпендикуляр b к плоскости α (по теореме о перпендикуляре к плоскости : если прямая перпендикулярна плоскости, то её проекции перпендикулярны к наклонным проекциям горизонтали и фронтали, лежащих в плоскости: b 2 ⊥f 2 ; b 1 ⊥h 1 ;
- Задаём плоскость β любым способом, например, β = a∩ b , таким образом, плоскость, перпендикулярная к заданной, построена: α⊥β.

Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС
3.9. Задачи для самостоятельного решения
1. Задана плоскость α = m //n (Рисунок 3.24). Известно, что K ∈α.
Постройте фронтальную проекцию точки К .

Рисунок 3.24
2. Постройте следы прямой, заданной отрезком CB , и определите квадранты, через которые она проходит (Рисунок 3.25).

Рисунок 3.25
3. Постройте проекции квадрата, принадлежащего плоскости α⊥π 2 , если его диагональ MN //π 2 (Рисунок 3.26).

Рисунок 3.26
4. Построить прямоугольник ABCD с большей стороной ВС на прямой m , исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).

Рисунок 3.27
5. Задана плоскость α=a //b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.

Рисунок 3.28
6. Задана плоскость α=∆АВС и точка D D плоскость β⊥α и β⊥π 1 .
7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE //α и DE //π 1 .
Чтобы прямая лежала в данной плоскости, необходимо, чтобы эта прямая имела с плоскостью две общие точки, которые и определят эту прямую.
Возьмем на данных прямых две произвольно расположенные точки Е
и F
(Е 1 Е 2
и F 1 F 2
) и проведем через них прямую k
(k 1
и k 2
). Эта прямая будет расположена в данной плоскости, так как она имеет с ней две общие точки (фиг.232,б).
Изображение на комплексном чертеже прямой, расположенной в плоскости, заданной следами:
а)
Возьмем на следах k
и L
произвольно точки М
(М 1 М 2
) и N
(N 1 N 2
) как следы прямой (фиг.233,а).
б)
Проведем через одноименные фронтальные (М 2
и N 2
) и горизонтальные (М 1
и N 1
) проекции точек М
и N
прямые (фиг.233,б).
Прямая MN
будет расположена в плоскости а как имеющая с ней две общие точки.
Отсюда следует: для того чтобы прямая принадлежала плоскости, надо, чтобы следы прямой лежали на одноименных следах этой плоскости.

Прямая лежит в плоскости, если имеет с ней одну общую точку и параллельна прямой, лежащей в плоскости. Пусть задана плоскость (фиг.234,а) прямой АВ
(А 1 В 1
и A 2 В 2
) и точкой С
(C 1 C 2
).
Требуется в заданной плоскости провести прямую через заданную точку С
.
Проведем через точку С
(С 1 С 2
) прямую параллельно прямой АВ
(А 1 В 1
и А 2 В 2
); эта прямая будет расположена в данной плоскости, так как она имеет с плоскостью общую точку и параллельна прямой, лежащей в данной плоскости (фиг.234,б).
Изображение на комплексном чертеже прямой
, расположенной в плоскости и параллельной одному из следов плоскости. Для проведения прямой в заданной следами плоскости а общего положения (прямая должна быть параллельна горизонтальному следу k
данной плоскости), возьмем на следе L
произвольную точку N (N 1 N 2
) как точку, лежащую в данной плоскости а (фиг.235,а).
След k
принимаем за прямую, лежащую в плоскости П 1
Проведем прямую через точку N 1
параллельно прямой k 1
получим горизонтальную проекцию h 1
прямой h
. Фронтальная проекция h 2
прямой h
пройдет через точку N 2
и расположится параллельно оси х 12
как прямая, параллельная плоскости П 1
(фиг.235,б).
Прямая h
будет принадлежать плоскости а
, как имеющая с ней общую точку (след N
) и параллельная прямой (следу к
), лежащей в данной плоскости.
Аналогичное построение будет справедливо и для случая, когда требуется провести прямую в заданной следами плоскости общего положения параллельно фронтальному следу L
(фиг.235,в и г).
Прямая h
, лежащая в плоскости а
, параллельная горизонтальной плоскости проекций П 1
, называется горизонталью данной плоскости (фиг.235,а и б).
Прямая f
, лежащая в плоскости а
, параллельная фронтальной плоскости проекций П 2
, называется фронталью данной плоскости (фиг.235,в и г).
Отсюда следует, что через всякую точку, лежащую в данной плоскости, можно провести одну горизонталь и одну фронталь. Разобрав различные изображения прямой в плоскости, можно на комплексном чертеже решить обратную задачу, т. е., имея проекции прямой, провести через нее соответствующую плоскость.

Пример 1.
Через данный отрезок АВ
(А 1 В 1 А 2 В 2
) провести плоскость общего положения и показать проекции следов этой плоскости (фиг. 236,а).
Зная, что следы прямой должны лежать на одноименных следах плоскости, сначала находим следы прямой, затем выбираем в произвольном месте на оси х 12
точку F 12
схода следов (фиг. 236,б) и, наконец, проводим следы плоскости общего положения (фиг. 236,в).
Пример 2.
Через данный отрезок АВ
(А 1 В 1 , А 2 В 2
) провести горизонтально - проектирующую плоскость и показать ее проекцию.
Так как в этом случае горизонтальная проекция прямой должна сливаться с горизонтальной проекцией плоскости, проводим горизонтальную проекцию σ 1
плоскости через горизонтальную проекцию прямой (фиг. 237).
Точка в плоскости. В случае изображения на комплексном чертеже проекций точки, лежащей в данной плоскости, сначала проводят в плоскости вспомогательную прямую, а затем на ней изображают точку.
а)
Построить проекции произвольной точки A
, принадлежащей плоскости а
, заданной следами (фиг.238,а).
Воспользуемся фронталью данной плоскости а
как прямой, лежащей в плоскости. Спроектируем одну из фронталей плоскости а
, например f
(f 1 , f 2
) (фиг.238,б).
Затем на фронтали проектируем произвольную точку, которую принимаем за заданную точку А
(А 1 A 2
) (фиг.238,в).
Так как обе проекции А 1
и А 2
точки А
лежат на проекциях фронтали f
плоскости а
, то, следовательно, точка А
лежит в заданной плоскости а
.
Таким же способом можно выполнить построение, воспользовавшись горизонталью h
(фиг.238,г)
б)
Пусть плоскость задана двумя пересекающимися прямыми АВ
(A 1 B 1 , A 2 A 2
) и ВС (B 1 C 1 , В 2 С 2
), требуется найти проекции D 1
и D 2
точки D
лежащей в заданной плоскости вне этих прямых (фиг.239,а). Зная, что проекции точки должны лежать на проекциях прямой, принадлежащей данной плоскости, проводим вспомогательную прямую EF
(E 1 F 1 , E 2 F 2
) так, чтобы она лежала в данной плоскости (фиг.239,б). Затем на прямой EF
(фиг.239,в) проектируем точку D
(D 1 D 2
).

Так как точка D
(D 1 D 2
) лежит на прямой EF
(E 1 F 1 , E 2 F 2
), находящейся в заданной плоскости, следовательно, она принадлежит заданной плоскости.
в)
Пусть плоскость σ
задана фронтальной проекцией σ 2
. Требуется построить проекции произвольной точки А
, принадлежащей данной плоскости.
Так как плоскость σ
- фронтально - проектирующая, то по свойству проектирующих плоскостей фронтальная проекция точки, лежащей в этой плоскости, должна сливаться с фронтальной проекцией данной плоскости.
Спроектируем произвольную точку А
так, чтобы фронтальная проекция A 2 точки лежала на проекции σ 2
, это и определит, что точка A
(A 1 A 2
) лежит в заданной плоскости (фиг.240).
Такое построение будет справедливо и для остальных проектирующих плоскостей.
Рассмотрим несколько примеров.
Пример I
. Дан треугольник AВС
(А 1 В 1 С 1 , A 2 B 2 C 2
) и произвольно расположенная точка D
(фиг.241,а); требуется определить, лежит ли точка D
(D 1 D 2
) в плоскости данного треугольника? Порядок проверки указан цифрами на (фиг.241,б).
1
- проводим через точки С 2
и D 2
прямую, получаем точку K 2
;
2
- проводим вертикальную линию связи, получаем точку К 1
;
3
- проводим через точки С 1
и К 1
прямую; в данном случае она прошла через точку Ьъ следовательно, точка D
(D 1 D 2
) лежит на прямой СК
(С 1 К 1 , С 2 K 2
), так как ее проекции лежат на проекциях этой прямой и на одной линии связи; прямая СК
принадлежит плоскости треугольника ABC
(A 1 B 1 C 1
, А 2 В 2 С 2
), так как имеет с ней две общие точки; следовательно, точка D
принадлежит плоскости треугольника.
Пример II
. Дан треугольник ABC
и расположенная произвольно прямая EF
(Е 1 F 1
E 2 F 2
), требуется определить, лежит ли прямая в плоскости данного треугольника (фиг.242,а)?
Порядок проверки указан цифрами на (фиг.242,б):
1
- продолжаем отрезок E 2 F 2
; в пересечении с прямыми В 2 А 2
и А 2 С 2
получаем точки Р 2
и Т 2
;
2
- проводим через точки Р 2
и Т 2
вертикальные линии связи до пересечения с прямыми В 1 А 1
и А 1 С 1
получаем точки Р 1
и Т 1
;
3
- проведем через точки Р 1
и T 1
прямую; в данном случае прямая сливается с отрезком E 1 F 1
следовательно, прямая РТ
принадлежит плоскости треугольника, так как одноименные проекции точек Р
и Т
лежат на одноименных проекциях прямых ВА
и АС
, принадлежащих треугольнику, и на одной линии связи; следовательно, прямая EF
принадлежит плоскости данного треугольника.
Точка принадлежит прямой, если её проекции лежат на одноимённых проекциях этой прямой (рис. 21а).
Точка принадлежит плоскости, если она лежит на прямой, лежащей в этой плоскости (рис.21б).
Прямая принадлежит плоскости, если она проходит через две точки, лежащие в этой плоскости (рис.21в).
Прямая параллельна плоскости, если она параллельна любой прямой, лежащей в этой плоскости. На рисунке 22 изображена прямая t, параллельная прямой b, принадлежащей плоскости Σ: t // b Î Σ (aÇ b).

Рисунок 22
Через любую точку пространства можно провести бесконечное множество прямых, параллельных данной плоскости.
Это задача на определение общей точки прямой и плоскости. Её называют также точкой встречи. Рассмотрим пересечение прямой с плоскостью частного положения.
Плоскость Σ задана треугольником АВС и является горизонтально проецирующей плоскостью. Точка встречи прямой k с плоскостью Σ определяется по горизонтальной проекции. Фронтальная проекция точки К достраивается с помощью линии связи. Символическая запись будет выглядеть следующим образом: k Ç Σ (ABC) = K.
Видимость прямой относительно плоскости определяется при помощи фронтально-конкурирующих точек 1 и 2.

Рисунок 23
Пересечение прямой с плоскостью общего положения изображено на рисунке 24. В этом случае нужно заключить прямую в проецирующую плоскость.
t Î Σ ^ П 2 - прямая t принадлежит плоскости Σ, которая перпендикулярна горизонтальной плоскости проекций. Линия пересечения этой плоскости с данной - линия (1, 2). Затем находится точка пересечения этой линии с прямой t , которая и будет являться точкой встречи прямой и плоскости. Видимость прямой относительно плоскости определяется при помощи конкурирующих точек. Возьмем горизонтально конкурирующие точки 3 и 4. Так как точка 3, принадлежащая прямой, оказалась ниже чем точка 4, следовательно, прямая на горизонтальной плоскости справа от точки пересечения невидима. Затем берем фронтально конкурирующие точки 1 и 5. Точка 1, принадлежащая плоскости, лежит ближе, следовательно, прямая находится за плоскостью, и она на фронтальной проекции невидима от точки 1 до точки К.

Рисунок 24
К особым прямым, принадлежащим плоскости, относятся горизонталь, фронталь и профильная прямая. Построение этих прямых используется при решении многих задач по начертательной геометрии. Их изображение дано на рисунке 25. Причём на горизонтальной плоскости горизонталь имеет натуральную величину, на фронтальной плоскости - фронталь и на профильной плоскости - профильная прямая.

Рисунок 25
1. Сформулируйте условия принадлежности точки плоскости и прямой плоскости.
2. Как построить прямую параллельную заданной плоскости?
3. Вспомните этапы решения задачи на определение точки пересечения прямой и плоскости.
4. Какие точки называются конкурирующими?
5. Как провести в плоскости горизонталь и фронталь?
6. Какие еще особые прямые плоскости вы знаете?
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек (а || )
Признак параллельности прямой и плоскости.
Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости.
Выводы.
Случаи взаимного расположения прямой и плоскости:
А) прямая лежит в плоскости;
б) прямая и плоскость имеют только одну общую точку;
в) прямая и плоскость не имеют ни одной общей точки.
Случаи взаимного расположения плоскостей:
Свойства параллельных плоскостей:
Задачи и тесты по теме "Тема 3. "Параллельность прямой и плоскости; параллельность плоскостей"."
- Параллельность плоскостей
Уроков: 1 Заданий: 8 Тестов: 1
- Параллельность прямых, прямой и плоскости - Параллельность прямых и плоскостей 10 класс
- Признаки параллельности двух прямых. Аксиома параллельных прямых - Параллельные прямые 7 класс
Уроков: 2 Заданий: 11 Тестов: 1
- Взаимное расположение прямых в пространстве. Угол между прямыми - Параллельность прямых и плоскостей 10 класс
Уроков: 1 Заданий: 9 Тестов: 1
- Перпендикулярность прямой и плоскости - Перпендикулярность прямых и плоскостей 10 класс
Уроков: 1 Заданий: 10 Тестов: 1
Тема "Аксиомы стереометрии" играет важную роль в развитии пространственных представлений, поэтому старайтесь привлекать больше моделей (картон и спицы), рисунков.
В теме "Параллельность в пространстве" даются знания о параллельности прямых и плоскостей в пространстве. В данном материале обобщаются известные из планиметрии сведения о параллельности прямых. На примере теоремы о существовании и единственности прямой, параллельной данной, Вы получаете представление о необходимости заново доказать известные из планиметрии факты в тех случаях, когда речь идет о точках и прямых пространства, а не о конкретной плоскости.
Задачи на доказательство решаются во многих случаях по аналогии с доказательством теорем. Для решения задач на вычисление длин отрезков необходимо провести повторение курса планиметрии: равенства и подобия треугольников, определений, свойств и признаков прямоугольника, параллелограмма, ромба, квадрата, трапеции.